Με απλούς γρίφους, προβλήματα μαθηματικών και ερωτήσεις σκέψης - λογικής θα σας κολλήσει στο πληκτρολόγιο του κινητού σας όποια ηλικία και αν είστε! Οι απαντήσεις σας είναι ευπρόσδεκτες στα σχόλια της ανάρτησης.
Όποιος επιθυμεί να στείλει το δικό του γρίφο κτλ. να το προωθήσει στο email
Οι λύσεις να δίνονται στα σχόλια της παρούσας ανάρτησης (μόνο σε πολύπλοκη λύση να στέλνεται με email).
Λύση στην εικασία Duffin-Schaeffer, έδωσε ο Έλληνας μαθηματικός Δημήτρης Κουκουλόπουλος, η επιστημονική πορεία του οποίου τον έφερε από το Μαθηματικό του Αριστοτελείου στο Σικάγο και το Πρίνστον.
Ο Κουκουλόπουλος, μόλις 35 ετών, με καταγωγή από την Κοζάνη, είναι σήμερα αναπληρωτής καθηγητής στο πανεπιστήμιο του Μόντρεαλ. Μαζί με τον συνεργάτη του Τζέιμς Μέιναρντ από την Οξφόρδη, κατάφεραν να αποδείξουν την εικασία που ταλάνιζε τους μαθηματικούς της Αναλυτικής Θεωρίας των Αριθμών εδώ και 78 χρόνια.
Και δεν είναι καν ο πιο παλιός γρίφος που παιδεύει τους μαθηματικούς. Εικασίες όπως αυτή του Πουανκαρέ ή το Τελευταίο Θεώρημα του Φερμά απασχολούσαν τους μαθηματικούς για δύο και τρεις αιώνες μέχρι να δοθεί ικανοποιητική λύση.
Σε συνέντευξή του στο ΑΠΕ, ο Δημήτρης Κουκουλόπουλος εξήγησε σε τι συνίσταται η εικασία και μίλησε για τις εφαρμογές της. Μίλησε ακόμη για το ελληνικό πανεπιστήμιο που του έδωσε τα εφόδια να φτάσει στην ανακάλυψή του, αλλά και για το brain drain που απειλεί την τριτοβάθμια εκπαίδευση στη χώρα μας.
Η εικασία διατυπώθηκε από τον Ντάφιν και τον Σάφερ το 1941 και αναφέρει τα κριτήρια που μπορούμε να θέσουμε ώστε να προσεγγίσουμε αριθμούς εάν απαγορεύσουμε κάποιους παρονομαστές. Οι δύο μαθηματικοί εισήγαγαν επίσης μια λεπτομέρεια που λέει ότι, εάν απαγορεύσουμε κάποιους παρονομαστές ακόμη και ένα αραιό υποσύνολό τους αυτών, μπορεί κάποιοι αριθμοί να μην προσεγγιστούν ποτέ. Γύρω στο 1990, υπήρξαν κάποια μικρά αποτελέσματα για την επίλυση της αλλά η εικασία παρέμενε άλυτη μέχρι το 2019 που αποδείχτηκε πλήρως από τον Κουκουλόπουλο και τον Μέιναρντ, δίνοντας λύση σε ένα από τα κεντρικά προβλήματα στον τομέα της μετρικής διοφαντικής προσέγγισης. Ονομάζεται έτσι προς τιμήν του αρχαίου μαθηματικού Διόφαντου από την Αλεξάνδρεια.
Τέκνο της δημόσιας εκπαίδευσης, ο Κουκουλόπουλος αποφοίτησε από το 2ο ΓΕΛ Κοζάνης και στη συνέχεια εισήλθε στο Μαθηματικό του ΑΠΘ. «Μου άρεσαν τα μαθηματικά και οι αριθμοί και στην τελευταία τάξη του Λυκείου έλαβα μέρος στον διαγωνισμό της Ελληνικής Μαθηματικής εταιρίας όπου κέρδισα το χάλκινο μετάλλιο», είπε στο ΑΠΕ και πρόσθεσε ότι το συγκεκριμένο γεγονός του πρόσφερε αυτοπεποίθηση και το ειδικό βάρος ώστε να διαλέξει την Μαθηματική Σχολή αντί του Πολυτεχνείου.
Μιλά με σεβασμό και αγάπη για δύο καθηγητές του και τη συμβολή τους στη διαμόρφωση των κριτηρίων και των δεξιοτήτων του. «Ο Αθανάσιος Κοζικόπουλος ήταν ο μαθηματικός μου στο Πειραματικό Γυμνάσιο Κοζάνης, ένας άνθρωπος με πάθος για τα μαθηματικά που κατάφερε τελικά να μου μεταδώσει για τα καλά το μικρόβιο και ο καθηγητής Μαθηματικών του ΑΠΘ Δημήτρης Μπετσάκος ήταν εκείνος που συνομίλησα μαζί του πριν αποφασίσω τελικά τι να επιλέξω».
Στο τελευταίο έτος του ΑΠΘ έκανε αιτήσεις για να πάει στις ΗΠΑ επιλέγοντας να πάει απευθείας για διδακτορικό στο πανεπιστήμιο του Ιλινόις «γιατί εκεί έχει μια πολύ καλή ομάδα στην Αναλυτική θεωρία των αριθμών που είναι ο τομέα της έρευνας μου». Προσθέτει: «Ήμουν αρκετά τυχερός γιατί εκεί άρχισα να δουλεύω με τον Kevin Ford έναν καθηγητή που είναι κορυφαίος στον τομέα του».
Τον τελευταίο χρόνο του διδακτορικού ακολούθησε τον μέντορα του στο «ναό» της Αναλυτικής Θεωρίας, στο πανεπιστήμιο του Πρίνστον. Η εμπειρία του εκεί φαίνεται ότι επηρέασε ακόμη περισσότερο τον Κουκουλόπουλο αφού εκεί γνώρισε τους πιο σημαντικούς επιστήμονες στο τομέα του. Το 2012 σε ηλικία μόλις 28 ετών προσελήφθη ως επίκουρος καθηγητής στο πανεπιστήμιο του Μόντρεαλ και σήμερα, μόλις 35 ετών, είναι αναπληρωτής καθηγητής στο ίδιο πανεπιστήμιο. Είναι κατηγορηματικός για το ότι το ελληνικό πανεπιστήμιο προσέφερε τα κατάλληλα επιστημονικά εφόδια. «Όταν πήγα στις ΗΠΑ δεν ένοιωσα κανένα μειονέκτημα σε σχέση με τους συμφοιτητές μου, ήμουν πλήρως προετοιμασμένος, είχα όλα τα εφόδια για να κάνω έρευνα γιατί στην Ελλάδα είχα πολύ καλούς δασκάλους και τα μαθηματικά που ήταν να μάθω, τα έμαθα».
Πιστεύει ότι η κρίση έχει τρομακτικό αντίκτυπο στα ελληνικά πανεπιστήμια αφού συνταξιοδοτήθηκαν αρκετοί καθηγητές χωρίς να αναπληρωθούν από νέο επιστημονικό αίμα. «Τα τελευταία δύο χρόνια μού λένε συνάδελφοί μου ότι άρχισαν να προσλαμβάνουν καθηγητές αλλά δεν υπάρχουν χρήματα για διδακτορικά προγράμματα κι αυτό έχει σαν αποτέλεσμα πολλοί νέοι να φεύγουν για το εξωτερικό και να μην επιστέφει κανένας πίσω».
Χαρακτηρίζει το φαινόμενο της φυγής των νέων επιστημόνων ως το κορυφαίο πρόβλημα της χώρας, θεωρεί ότι η Ελλάδα έχει καθοδική πορεία που πρέπει να αναστραφεί επειγόντως και να επιστρέψουν ορισμένοι από τους ανθρώπους που έφυγαν. Εξηγεί: «Πρέπει να αλλάξει ο τρόπος λειτουργίας των πανεπιστήμιων, να πλησιάσει το πλαίσιο λειτουργίας των ευρωπαϊκών και αμερικάνικων πανεπιστήμιων, να είναι αυτοδύναμα και να αποφασίζουν τα ίδια πού θέλουν να πάνε την έρευνα τους».
Σχολίασε ακόμη την ανάμειξη της κεντρικής κυβέρνησης στην ίδρυση και στην κατάργηση της Νομικής Σχολής της Πάτρας και αναρωτήθηκε γιατί ο υπουργός πρέπει να αποφασίζει εάν η Πάτρα θα πρέπει να έχει Νομική σχολή, αφού αυτό είναι καθαρά θέμα του πανεπιστημίου. Αναφέρθηκε με θετικό πρόσημο στον νόμο Διαμαντοπούλου και στα συμβούλια των ιδρυμάτων, που όμως καταργήθηκαν, θεωρώντας ότι ήταν ένα μεγάλο βήμα για τα ελληνικά πανεπιστήμια, ενώ αναφέρθηκε με επικριτικό τόνο στην παρουσία και τον έλεγχο που ασκούν οι παρατάξεις στη διοίκηση του πανεπιστήμιου δηλώνοντας ότι «ουσιαστικά, οι σύγκλητοι των πανεπιστημίων είναι όμηροι των παρατάξεων».
Με την εμπειρία των αμερικανικών πανεπιστημίων ο Δημήτρης Κουκουλόπουλος θεωρεί ότι το σύστημα ελέγχου και διοίκησης των ελληνικών πανεπιστημίων είναι απόλυτα εξαρτώμενο από την κεντρική διοίκηση, όπου ο υπουργός αποφασίζει για πολλά. «Όταν το υπουργείο αποφασίζει τους μισθούς των πάντων τότε όλα γίνονται δύσκολα. Όσο πιο κεντρικά γίνεται κάτι, τόσο πιο δύσκολα θα έχεις ευελιξία. Ευελιξία και εμπιστοσύνη χρειάζεται και να είμαστε σίγουροι ότι οι άνθρωποι θα κάνουν σωστά τη δουλειά τους».
Υποστηρικτής της αξιολόγησης, θεωρεί ότι η εφαρμογή της πρέπει να υποστηρίζει θετικά το έργο των πανεπιστημιακών, ώστε να κάνουν καλύτερα τη δουλειά τους. Υποστηρικτής, ακόμη, και της μονιμότητας στο πανεπιστήμιο γιατί όπως λέει «οι καθηγητές δεν πρέπει να φοβούνται ότι κάποια στιγμή θα κινδυνεύσουν να απολυθούν γιατί πολλές φορές ορισμένα πρότζεκτ χρειάζεται μια ολόκληρη ακαδημαϊκή ζωή για να τα φέρεις σε πέρας».
37) 23/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2018 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Ποιο σχήμα μπορείτε να κατασκευάσετε ενώνοντας τα παρακάτω κομμάτια;
36) 22/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2018 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Ο Ιερεμίας έχει δημιουργήσει μια εφαρμογή για έξυπνα κινητά, που την ονομάζει «Δημιουργό Αριθμητικών Παραστάσεων». Πρέπει να χρησιμοποιήσετε και τα τέσσερα μαθηματικά σύμβολα (+, -, : και x) με όποια σειρά θέλετε, έτσι ώστε ξεκινώντας από τον αριθμό 7 να καταλήξετε στον αριθμό 144.
35) 21/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2018 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
 Εκφώνηση:
Εκφώνηση: Μπορείτε να βρείτε ποιο από τα αυτοκίνητα ανήκει σε ποιον;
Γνωρίζετε τις εξής πληροφορίες;
• Κάποια από τα αυτοκίνητα αυτά χρησιμοποιούν αμόλυβδη βενζίνη ενώ άλλα όχι.
• Αυτά που δεν καταναλώνουν αμόλυβδη βενζίνη, παράγουν περισσότερα καυσαέρια.
• Ο Δημήτρης δεν χρησιμοποιεί αμόλυβδη βενζίνη, αλλά το αυτοκίνητό του έχει ραδιόφωνο. Οι ζάντες του είναι ίδιες με του Φώτη.
• Ο Ανδρέας έχει ραδιόφωνο στο αυτοκίνητό του και οι ζάντες του είναι ίδιες με αυτές του Στέφανου.
• Ο Στέφανος βάζει στο αυτοκίνητό του τον ίδιο τύπο καυσίμου που χρησιμοποιεί και ο Ευγένιος.
34) 20/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2018 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Συμπληρώστε τον πίνακα, ώστε το άθροισμα κάθε γραμμής και κάθε στήλης να είναι ίσο με τον αριθμό που φαίνεται στο εξωτερικό του.
33) 19/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2018 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Υπάρχει τρίγωνο με δύο ύψη μεγαλύτερα ή ίσα από τις πλευρές προς τις οποίες καταλήγουν; Αν ναι, ποιες είναι οι γωνίες του τριγώνου;
32) 18/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2018 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Ποιος αριθμός λείπει από την πόρτα στα δεξιά του σπιτιού;
31) 17/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2017 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Στο σχήμα βλέπετε ένα τραπέζιο. Αν φέρουμε μια κάθετη στο εσωτερικό του τραπεζίου, παρατηρούμε ότι εμφανίζεται ένα ολόκληρο τετράγωνο και το μισό του. Μπορείτε να χωρίσετε το τραπέζιο σε τέσσερα σχήματα που όλα να έχουν ακριβώς το ίδιο μέγεθος και μορφή;
30) 16/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2017 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Ο κύριος Αγαπητός (Α) χρωστάει 50 € στη δεσποινίδα Βαρώνου (Β), ενώ η κυρία Διαμάντη (Δ) χρωστάει 40 € στον κύριο Γαληνό (Γ) και ούτω καθεξής, όπως φαίνεται παρακάτω. Πώς μπορούν να διευθετηθούν αυτά τα πέντε χρέη με δύο απλές αποπληρωμές;
29) 15/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2017 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Τα γράμματα α και β παριστάνουν δύο ψηφία διαφορετικά από το μηδέν. Μπορείτε να τα προσδιορίσετε;
(Να βρείτε περισσότερες από μια απαντήσεις.)
28) 14/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2017 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Ακολουθώντας το μοτίβο των σχημάτων από τα αριστερά προς τα δεξιά, επιλέξτε ποιο από τα παρακάτω σχήματα είναι αυτό που ταιριάζει στο τέλος της γραμμής.
27) 13/8/2019
Άρθρο: Απόψε η βροχή των αστεριών
Η πιο θεαματική θερινή - αν όχι ετήσια - βροχή από «πεφταστέρια», οι διάττοντες Περσείδες, θα κορυφωθούν από απόψε τα μεσάνυχτα προς τα χαράματα της Τρίτης, στο νυχτερινό ουρανό της χώρας μας και γενικότερα του βορείου ημισφαιρίου.
Φέτος όμως, ακολουθεί πανσέληνος στις 15 Αυγούστου, με αποτέλεσμα η λάμψη από το μεγάλο φεγγάρι, που θα είναι αρκετά φωτεινό, να εμποδίσει σε ένα βαθμό την παρατήρηση των μετεώρων, έτσι θα γίνουν ορατά μόνο τα πιο φωτεινά από αυτά.
Οι Περσείδες είναι εντυπωσιακές βροχές διαττόντων, καθώς τα «πεφταστέρια» τους είναι γρήγορα και φωτεινά, διαθέτοντας συνήθως μακριές πύρινες «ουρές».
Αν τελικά αποφασίσετε να παρακολουθήσετε το όμορφο φαινόμενο προτείνουμε να το κάνετε σε μια περιοχή με χαμηλό φωτισμό και να μην εμποδίζεται η πλήρη παρακολούθηση του ουρανού! Δεν χάνετε τίποτα να βάλετε μια ευχή καθώς θα βλέπετε να πέφτουν τα ορατά εκατοντάδες αστέρια!
26) 12/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2017 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Τρεις γείτονες μοιράστηκαν το περιφραγμένο πάρκο που φαίνεται στην εικόνα. Σύντομα υπήρξε ένας μικροκαβγάς ανάμεσά τους. Ο ιδιοκτήτης του κεντρικού σπιτιού παραπονέθηκε ότι το σκυλί των γειτόνων έσκαψε στον κήπο του και κατασκεύασε αμέσως ένα περιφραγμένο μονοπάτι που οδηγεί στην έξοδο 1 της εικόνας. Ο ιδιοκτήτης του αριστερού σπιτιού κατασκεύασε ένα περιφραγμένο μονοπάτι που οδηγεί στην έξοδο 2, ενώ αυτός που μένει στο σπίτι δεξιά στην εικόνα κατασκεύασε ένα περιφραγμένο μονοπάτι που οδηγεί στην έξοδο 3. Να σχεδιάσετε τα μονοπάτια χωρίς αυτά να διασταυρώνονται.
 25) 11/8/2019
Πηγή:
25) 11/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2017 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Εφτά φοιτητές, οι οποίοι συγκατοικούν σ΄ ένα μεγάλο διαμέρισμα στο Εδιμβούργο της Σκωτίας, μοιράζονται εφτά διαφορετικές δουλειές του σπιτιού. Ο Γιώργος επινοεί αυτό τον γρίφο, ενώ προσπαθεί να σκεφτεί ένα εβδομαδιαίο πρόγραμμα για τους έξι συγκατοίκους του με σκοπό να βρεθεί ένας τρόπος, ώστε ο καθένας τους να κάνει κάθε δουλειά του σπιτιού μόνο μία φορά. Δίνει τον γρίφο στη συγκάτοικο του, την Αλίκη, και της λέει:
«Μπορείς να συμπληρώσεις το πλέγμα, έτσι ώστε κάθε γραμμή και στήλη, αλλά και κάθε περιγεγραμμένη περιοχή, να περιέχει τα γράμματα από το Α ως το Η;»
Ξεκινήστε από τη δεξιά ακριανή στήλη ή δοκιμάστε να βάλετε το Ζ στο κέντρο του πλέγματος.
 24) 10/8/2019
Πηγή:
24) 10/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2017 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Στα τετραγωνάκια του πίνακα να τοποθετήσετε τους φυσικούς αριθμούς από το 1 έως και το 12 με τρόπο ώστε :
α) το άθροισμα σε κάθε στήλη να είναι το ίδιο,
β) το άθροισμα σε κάθε γραμμή να είναι το ίδιο,
γ) στην πρώτη γραμμή οι αριθμοί να είναι διατεταγμένοι κατά αύξουσα σειρά.
 23) 9/8/2019
Πηγή:
23) 9/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2017 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Τρεις φίλοι μπαίνουν σε μία κάβα και αγοράζουν ένα μπουκάλι καλό κρασί που κοστίζει 30€ δίνοντας 10€ ο καθένας. Φεύγοντας, τους προλαβαίνει ο υπάλληλος και τους λέει πως έκανε λάθος γιατί το μπουκάλι στοιχίζει 25€ και όχι 30€ και γι’ αυτό τους επιστρέφει 5€ ρέστα. Αυτοί, αφού δε μπορούν να μοιράσουν τα 5€ στα τρία, παίρνουν ο καθένας από 1€ και δίνουν 2€ φιλοδώρημα στον υπάλληλο για την καλή του πράξη. Στο τέλος όμως σκέφτονται: Έδωσε ο καθένας μας 10€ και πήρε ένα πίσω, άρα 9€. Τρεις φορές το 9€ μας κάνει 27€ και 2€ για το φιλοδώρημα, 29€. Τι έγινε το 1€;
22) 8/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2017 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Τοποθετήστε στα κενά τετράγωνα τους αριθμούς 1 έως 9 , έτσι ώστε τα αποτελέσματα των πράξεων οριζόντια και κάθετα να είναι σωστά. Όλοι οι υπολογισμοί γίνονται από τα αριστερά προς τα δεξιά και από πάνω προς τα κάτω και εμπεριέχουν μόνο θετικά αποτελέσματα.
 21) 7/8/2019
Πηγή:
21) 7/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2017 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Ένας αθλητής πραγματοποιεί άλματα συνεχώς χωρίς σταματημό. Ωστόσο, σε κάθε νέο άλμα λόγω κούρασης προχωρά τη μισή απόσταση του προηγούμενου άλματος. Αν στο πρώτο του άλμα ο αθλητής έφτασε τα 5 μέτρα, πόσα άλματα θα χρειαστεί για να φτάσει τα 10 μέτρα;
20) 6/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2017 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Παρατήρησε την ακολουθία των παρακάτω αριθμών:
1, 11, 21, 1211, 111221, 312211 …
Οι όροι της δεν προκύπτουν από τον ή τους προηγούμενους όρους μετά από κάποιες αριθμητικές πράξεις. Ποιος είναι ο επόμενος αριθμός;
19) 5/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2017 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Ρώτησαν τον κ. Χάιντ να φανερώσει τον μυστικό εξαψήφιο αριθμό που χρησιμοποιούσε στον Η/Υ του και αυτός απάντησε ως εξής: Σας δίνω τρία στοιχεία:
1. Ο αριθμός διαβάζεται το ίδιο και από τα δεξιά και από τα αριστερά.
2. Είναι πολλαπλάσιο του 9.
3. Ο αριθμός που σχηματίζεται από τα τέσσερα μεσαία ψηφία έχει πρώτο παράγοντα μόνο το 11.
Βρείτε τον μυστικό αριθμό του κ. Χάιντ.
18) 4/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2017 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Ο κ. Μιχάλης αποφάσισε να κάνει δώρο στα ανίψια του, για τα γενέθλιά τους ένα παιχνίδι με αριθμούς. Έτσι κατασκεύασε τα εξάγωνα που βλέπετε στο σχήμα. Ο σκοπός είναι να τοποθετήσουν τα εξάγωνα στο κεντρικό πλέγμα, έτσι ώστε εκεί όπου το ένα εξάγωνο ακουμπά το άλλο κατά μήκος της έντονης γραμμής, θα πρέπει και τα δύο τρίγωνα να έχουν το ίδιο περιεχόμενο. Δεν επιτρέπεται η περιστροφή κανενός εξάγωνου. Μπορείτε να τους βοηθήσετε;
 17) 3/8/2019
Πηγή:
17) 3/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2017 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Ποιος αριθμός λείπει;
 16) 2/8/2019
Πηγή:
16) 2/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2017 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Ο Αχιλλέας και η χελώνα έτρεξαν σε μία κούρσα 100 μέτρων. Όταν ο Αχιλλέας τερμάτισε, η χελώνα βρισκόταν 20 μέτρα πριν από τον τερματισμό. Ο Αχιλλέας πρότεινε στην χελώνα να ξανατρέξουν, αλλά αυτή τη φορά θα ξεκινούσε 20 μέτρα πιο πίσω από την γραμμή της αφετηρίας. Αν κρατηθούν όλες οι συνθήκες ίδιες, θα κερδίσει ο Αχιλλέας, η χελώνα ή θα τερματίσουν ταυτόχρονα;
15) 1/8/2019
Πηγή: Από τους μαθηματικούς διαγωνισμούς 2017 Γυμνασίου της Εκπαιδευτικής Αναγέννησης. Μας τα πρόσφερε ο αγαπητός φίλος και συνάδελφος Κωνσταντίνος Λάττας
Εκφώνηση: Μπορείς να μετακινήσεις ένα σπίρτο ώστε να προκύψει αληθής σχέση;
14) Διάταξη - Άσκηση [31/7/2019]
Πηγή: Παραποιημένο θέμα από τις σημειώσεις του καθηγητή Πανεπιστημίου
Ανδρέα Μπούκα που έχει τη λέξη
"M I S S I S S I P P I"
Εκφώνηση: Με πόσους διαφορετικούς τρόπους μπορούμε να διατάξουμε τα γράμματα της λέξης
"l i s a r i"
13) Παλίνδρομοι αριθμοί - άσκηση [30/7/2019]
Πηγή: Τέθηκε σε φοιτητές των ΗΠΑ και μόλις το 2% τους κατέγραψε όλους!
Εκφώνηση: "
Να βρείτε όλους τους παλίνδρομους πενταψήφιους αριθμούς που διαιρούνται με το 45".
Απάντηση: Οι ζητούμενοι αριθμοί είναι μόνο δέκα και είναι οι εξής:
50805, 51615, 52425, 53235, 54045, 55755, 56565, 57375, 58185, 59895
12) Παλίνδρομοι αριθμοί - άρθρο [30/7/2019]
Πηγή: https://blogs.sch.gr/imavros/files/2011/02/024.pdf
Παλινδρομικοί αριθμοί είναι αυτοί που διαβάζονται το ίδιο είτε ευθέως είτε ανάποδα. Για παράδειγμα, οι αριθμοί 565, 13231, 1234321 κλπ. Επιλέγουμε έναν τυχαίο αριθμό, για παράδειγμα το 83. Τον αντιστρέφουμε και τον προσθέτουμε στον αρχικό μας αριθμό. Έχουμε δηλαδή 83+38=121 Έναν παλινδρομικό δηλαδή αριθμό. Επιλέγουμε έναν άλλο τυχαίο αριθμό, για παράδειγμα το 67. Τον αντιστρέφουμε και τον προσθέτουμε στον αρχικό μας αριθμό. Έχουμε δηλαδή 67+76=143. Επαναλαμβάνουμε την διαδικασία κι έχουμε 143+341=484. Έναν παλινδρομικό δηλαδή αριθμό. Η ιδιότητα αυτή που έχουν οι αριθμοί, να καταλήγουν σε παλινδρομικούς μετά από μερικές προσθέσεις με τον αντεστραμμένο εαυτό τους φαίνεται να ισχύει για όλους. Υπάρχουν όμως μερικοί αριθμοί για τους οποίους ακόμα δεν έχουμε καταλήξει σε παλίνδρομο παράγωγό τους. Ο μικρότερος από αυτούς, είναι το 196. Κατόπιν πολλών πράξεων, φτάσαμε σε αριθμό με 263.000.000 ψηφία, ο οποίος όμως δεν ήταν παλίνδρομος. Για αριθμούς μικρότερους του 10.000 απαιτούνται το πολύ 24 προσθέσεις και το ρεκόρ αυτό κατέχει ο αριθμός 89.
11) Γρίφος - κουτσομπολιό [29/7/2019]
Επειδή οι συζητήσεις για την επιτροπή εξετάσεων κτλ. καλά κρατεί κάθε χρόνο (αν και δεν βρίσκω λόγο γιατί συμβαίνει) τους προτείνω να ασχοληθούν με τον παρακάτω γρίφο! Είναι κυρίως για τα άτομα που δίνουν σημασία στα ονόματα και στην ιστορία!
"Ποιος ήταν ο Καθηγητής Πανεπιστημίου που ηγήθηκε στην επιτροπή των Μαθηματικών στις φετινές Πανελλαδικές Εξετάσεις 2019 και επίσης είχε ξανά ηγηθεί το 2013 (και όχι μόνο);"
Οι απαντήσεις θα γίνονται δεκτές μόνο σε προσωπικό μήνυμα!
10) Εισιτήριο σε αστικό λεωφορείο - Άσκηση [28/7/2019]
Πηγή: Από τα ενδεικτικά θέματα του Πυθαγόρα για τάξεις Α΄ και Β΄ Γυμνασίου
9) Αγγλικά και Γαλλικά - Άσκηση [27/7/2019]
Πηγή: Από τα ενδεικτικά θέματα του Πυθαγόρα για τάξεις Α΄ και Β΄ Γυμνασίου
8) Βρείτε την περίμετρο - άσκηση [26/7/2019]
Πηγή: Μια άσκηση που έρχεται από το διαγωνισμό του "
Πυθαγόρα" 2018 - 19 για τις τάξεις Α΄ - Β΄ Γυμνασίου.
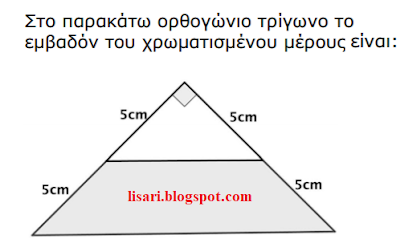
7) Βρείτε το εμβαδόν - άσκηση [25/7/2019]
Πηγή: Μια άσκηση που έρχεται από το διαγωνισμό του "
Πυθαγόρα" 2018 - 19 για τις τάξεις Α΄ - Β΄ Γυμνασίου.
6) Σεισμοί και καταποντισμοί - άσκηση [24/7/2019]
Χθες ο διευθυντής του Γεωδυναμικού Ινστιτούτου
Άκης Τσελέντης δήλωσε στο Έθνος ότι αναμένουμε 30 φορές πιο δυνατό σεισμό στην Αθήνα (σε σχέση με τον πρόσφατο σεισμό των 5,1 ρίχτερ). Άρα τι σεισμό αναμένει ο διευθυντής του Γεωδυναμικού Ινστιτούτου; Η απάντηση να δοθεί σύμφωνα με τη γνώση που έχουμε από το σχολικό βιβλίο Άλγεβρας της Β Λυκείου.
5) Blog - άρθρο [23/7/2019]
Περιηγηθείτε σε ένα ενδιαφέρον blog που ανακάλυψα πρόσφατα. Είναι το
Είναι ένα δημοφιλές blog με επίκεντρο την προστασία του Παιδιού. Μια αφιλοκερδής προσπάθεια που αξίζει να τη στηρίξουμε - επιβραβεύσουμε. Από σήμερα είμαστε αδελφοποιημένα blog!
4) Άσκηση lisari - Άσκηση [22/7/2019]
Πηγή: Παραποιημένο θέμα από τον Κυπριακό διαγωνισμό 2018 - 19 για τους μαθητές της Α΄ Γυμνασίου.
Εκφώνηση: Γράφουμε τη λέξη lisari επανειλημμένα χωρίς κενά και σχηματίζουμε το ακόλουθο μοτίβο γραμμάτων: lisarilisarilisarilisarilisarilisari … Να προσδιορίσετε, αιτιολογώντας την απάντησή σας το γράμμα που θα βρίσκεται στην 2019η θέση.
3) Κηπουρός και πεύκα - Άσκηση [21/7/2019]
Πηγή: Από τα ενδεικτικά θέματα του Πυθαγόρα για τάξεις Α΄ και Β΄ Γυμνασίου
Εκφώνηση - σχήμα:
2) Βρείτε το εμβαδόν - Άσκηση [20/7/2019]
Πηγή: Μια άσκηση που προέρχεται από τους διαγωνισμούς για την εισαγωγή στη Σχολή Δημόσιας Διοίκησης
Εκφώνηση - σχήμα:
1) Βρείτε το εμβαδόν - Άσκηση [19/7/2019]
Πηγή: Μια άσκηση που έρχεται από το διαγωνισμό του "
Πυθαγόρα" 2018 - 19 για τις τάξεις Α΄ - Β΄ Γυμνασίου και έχει αρκετούς τρόπους επίλυσης.
Εκφώνηση: Στο παρακάτω σχήμα είναι ένα τετράγωνο με περίμετρο 48 cm και είναι χωρισμένο σε μικρότερα ίσα τετραγωνάκια. Πόσα cm^2 είναι το εμβαδόν της σκούρας επιφάνειας;